怎么算那个的长度公式(怎么求弧的长度公式)

长度的计算在许多科学和工程领域具有重要意义。无论是测量物体的尺寸，还是进行复杂的数学计算，了解如何准确计算长度都是必备技能。本文将详细介绍长度计算的公式，帮助你掌握这一关键概念。

长度公式的基本定义

长度可以通过多种方式来计算，具体取决于所涉及的几何形状。最基本的长度计算公式通常涉及直线距离和周长。对于一条直线，其长度可以简单地用两点之间的距离公式来计算，即：

长度 = 终点坐标 - 起点坐标

这种方法适用于一维空间的直线距离计算。

复杂形状的长度计算

在处理更复杂的几何形状时，如圆、弧或多边形，长度计算公式会有所不同。对于圆形，周长公式为：

周长 = 2πr

其中，r是圆的半径。对于弧的长度，可以使用以下公式：

弧长 = θr

其中，θ是弧度，r是半径。而对于多边形的周长，可以通过求各边长之和来实现。

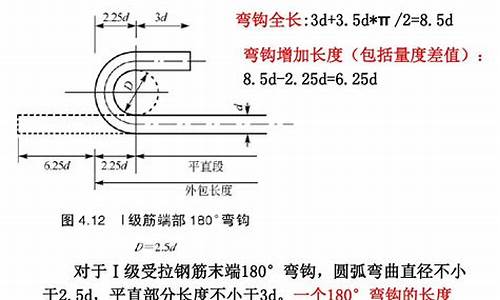
应用实例解析

为了更好地理解这些公式，我们来看一个实际应用实例。假设我们需要计算一条从点A(1,2)到点B(4,6)的直线段的长度。根据直线距离公式：

长度 = √((x2 - x1)² + (y2 - y1)²)

代入数据后得出：

长度 = √((4-1)² + (6-2)²) = √(9 + 16) = √25 = 5

由此可见，使用正确的公式可以轻松计算出长度。

总结，掌握长度计算的各种公式不仅仅是在学术领域中有用，在日常生活和工作中同样不可或缺。希望通过本文的讲解，能让你对长度计算有更全面的了解，并能灵活应用于实际问题中。